4. 图形的复合变换
上一小节我们通过对矩阵乘矢量的自行推导,实战了矩阵在 WebGL 中的应用,成功实现了图形的平移效果。那么这一节,我们继续深入矩阵在 WebGL 中的应用,实战图形平移+旋转的复合变换效果。
复合变换和矩阵
相信现在的你对于矩阵在 WebGL 中的妙用已经稍有体会了,毕竟平移、缩放、旋转都可以通过矩阵乘法来实现,并且其极大的简化我们着色器中的公式应用,实现一种着色器代码走天下的效果~那你又知不知道矩阵在复合变换中同样适用呢?
首先我们抛开矩阵,看看直接写表达式要怎么实现平移+旋转的复合变换。
const vertexCode = `
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
uniform float u_Rotate;
uniform vec4 u_Position;
void main () {
// 两矢量相加
gl_Position = vec4(
a_Position.x * cos(u_Rotate) - a_Position.y * sin(u_Rotate),
a_Position.x * sin(u_Rotate) + a_Position.y * cos(u_Rotate),
0.,
1.
) + u_Position;
v_Color= a_Color;
}
`那么根据 本章第 1 节 的等式,我们大概可以推出平移+旋转的着色器代码如上。这里我们把两个矢量进行相加,一个是计算旋转后的 vec4 坐标点,一个是平移产生的位移值 u_Position。
还是上一节说过的,通过数学等式的组合并不是不可以实现复合变换,只是针对每种变换我们都得实现一个对应的 shader,所以我们依然坚定地把目光转向矩阵!看看这个神奇的数学工具在复合变换中的应用!
既然是要实现平移+旋转的复合变换,那我们依然可以将其一一拆开来做一定的推导!回顾我们上一节用矩阵实战平移的核心着色器代码如下:
// 平移矩阵 x 顶点坐标
gl_Position = u_TranslateMatrix * a_Position;那其实对于旋转的变换,我们依然可以使用上述的矩阵乘法矢量的等式来实现,只是需要传入的矩阵跟平移的矩阵不一样而已。所以旋转的着色器核心实现依然是一样的等式:
// 旋转矩阵 x 顶点坐标
gl_Position = u_RotateMatrix * a_Position;虽然我们现在需要复合平移和旋转两种变换效果,但是从分解后来看,无非就是先平移一个顶点坐标然后再将其进行一定角度的旋转就可以实现了。那换算到上述的等式中,我们其实可以这样写:
// 旋转矩阵 x 平移后的坐标矢量
gl_Position = u_RotateMatrix * (u_TranslateMatrix * a_Position);那么回顾 矩阵乘法 小节,我们知道矩阵乘法遵循结合律。也就是上述等式我们可以换算成:
// (旋转矩阵 x 平移矩阵) x 顶点坐标
gl_Position = (u_RotateMatrix * u_TranslateMatrix) * a_Position;根据矩阵乘法的规则,我们两个 4x4 矩阵相乘的结果依然是一个 4x4 矩阵。所以上述等式可以再进一步推导回最初矩阵乘矢量的模式:
// 模型矩阵 x 顶点坐标
gl_Position = u_ModelMatrix * a_Position;上述代码中的 u_ModelMatrix 为 模型矩阵,这个模型矩阵是通过多个变换矩阵的结合得到的(本例中是平移和旋转矩阵的复合)。经历过一次次地推导,我们又回到了最初的起点——矩阵乘矢量。所以,现在你应该更深刻地体会到矩阵对于 WebGL 的意义了吧?
JavaScript与矩阵
经过上述推导,我们得到了最新的复合变换等式:
gl_Position = u_ModelMatrix * a_Position
这个等式跟上一节我们实现图形平移是一样的,只是 u_ModelMatrix 是通过复合多个变换后得到的矩阵而已。
这也就意味着,我们在 JavaScript 中计算好 平移矩阵 x 旋转矩阵 的值后,再传递给到着色器就可以实现图形的复合变换了。但是,JavaScript 并不像 GLSL 那样原生支持矩阵、矩阵乘法,要是再像上一小节那样手动写矩阵,然后还要运算他们的乘法就很蛋疼了...
所以这个时候,我不由自主的打开了 Google,找个库用去!(大前端最不缺的就是库!各种轮子要啥有啥)诶等等,上一节不是在 three.js 库中看到了 Matrix4 的类吗?那,那还找毛啊,直接用啊!
初探THREE.Matrix4源码
因为它源码里面的命名(各种英文直接搜)都比较好理解,所以我们完全可以看源码来操作!这里贴上对应的 官方文档-Matrix4 ,有需要的同学可以去看文档来使用。
ok,现在我们先来简单地看看这玩意的源码吧。比如上一节我截了它构造器的实现:
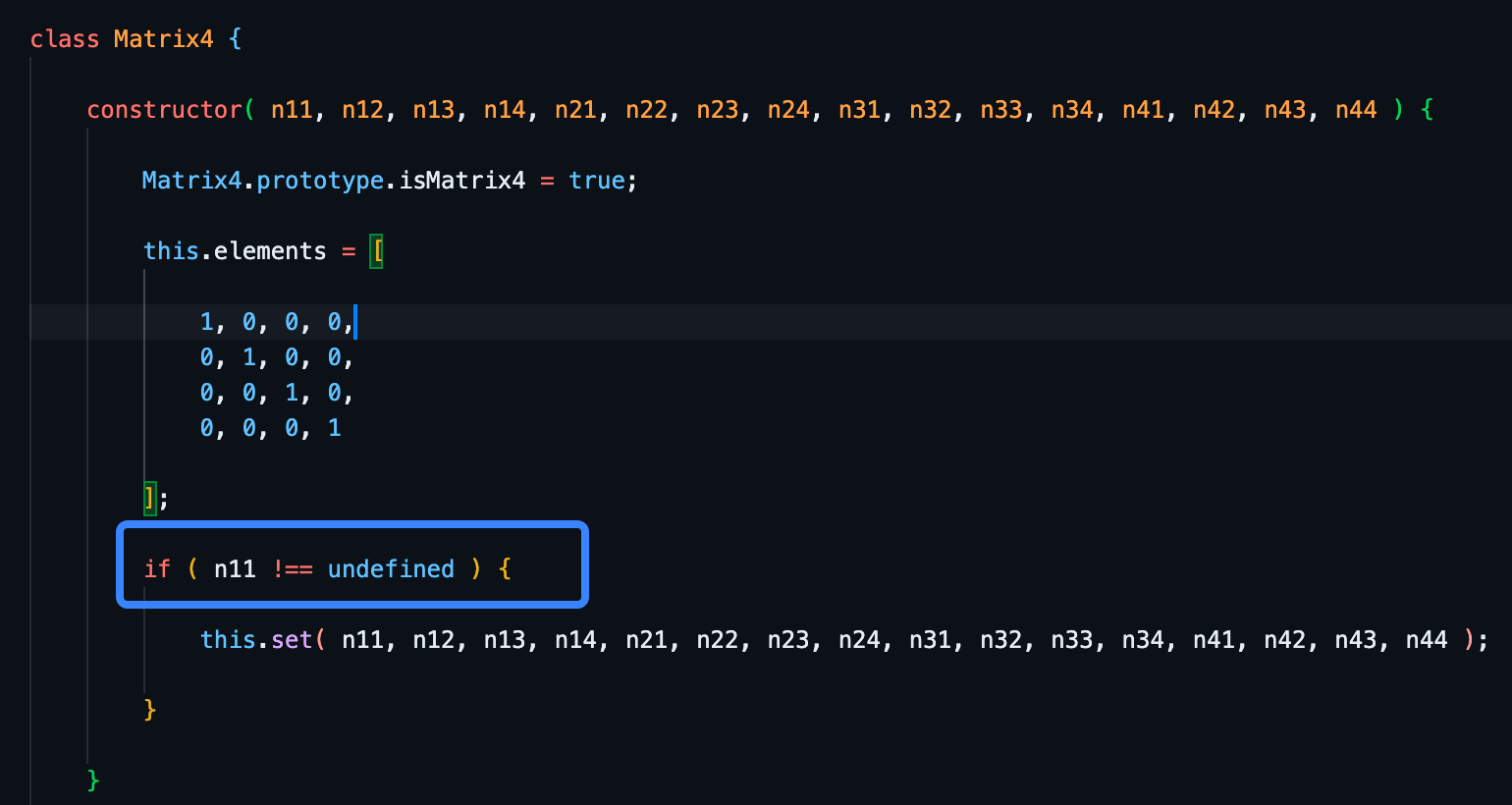
可以看到,当我们什么都不传直接 new 的时候,可以得到一个 单位矩阵 在 elements 这个属性里!因为我们要实现平移和旋转,所以接下来我们着重看看有没有跟 translate 和 rotate 相关的代码!
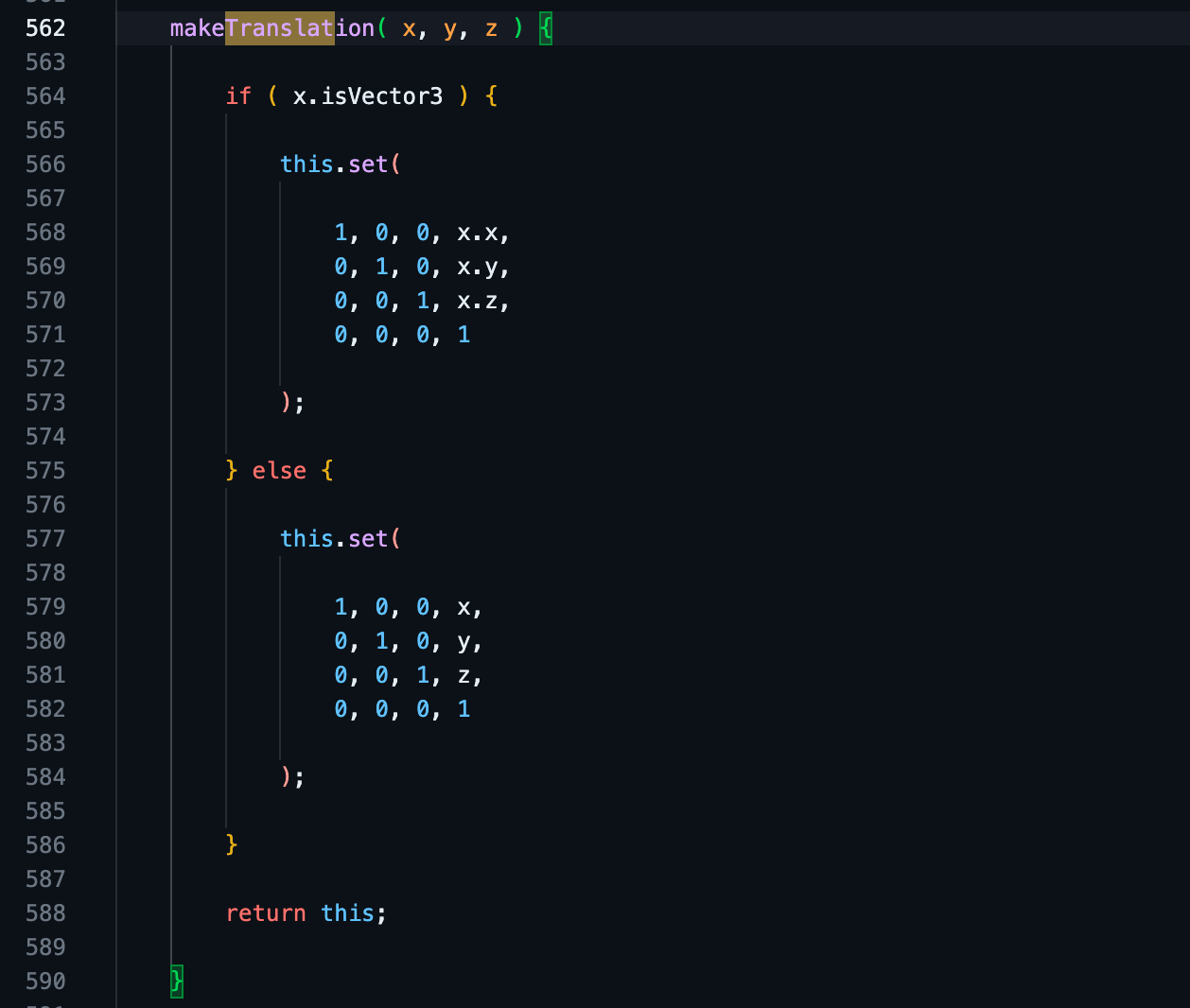
果不其然,很快我就找到了 makeTranslation 函数。从图中一看我们发现实现其实很简单,就是根据参数帮我们把 x、y、z 放到对应的平移变换矩阵的位置中!这个矩阵我们非常熟悉了,毕竟在上一节我们是亲自推导出来的,忘记的可以回顾一下:
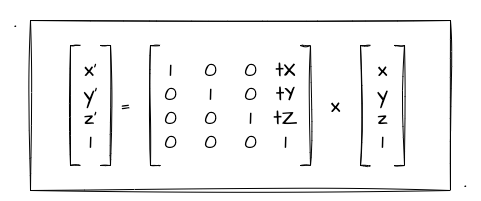
接着我们继续寻找旋转相关的,找到如下截图:
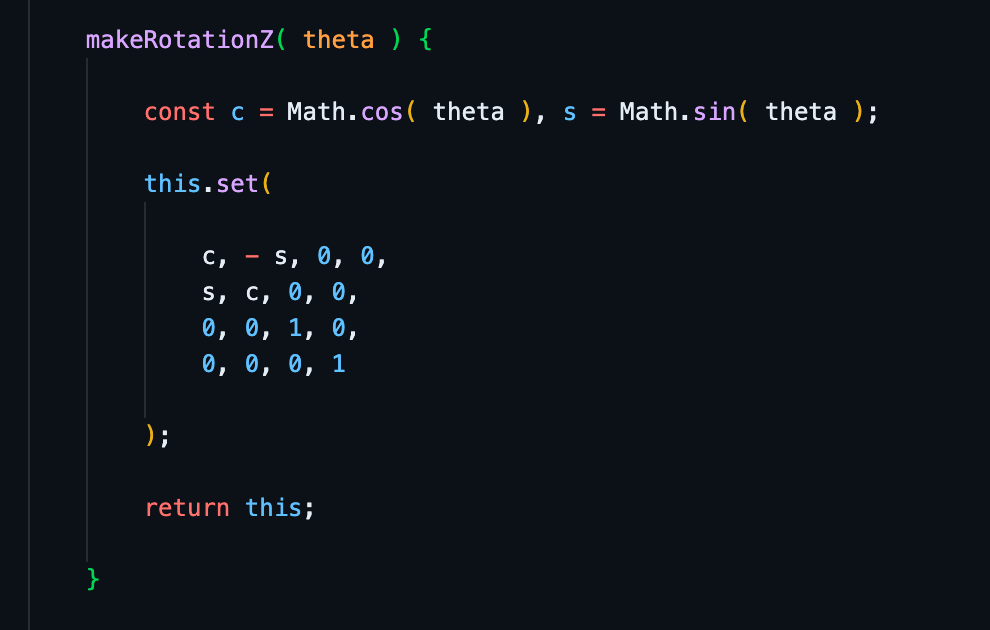
源码也是非常简单了,用 Math.cos 和 Math.sin 计算好余弦正弦值再放到旋转的变换矩阵中。忘记为什么要求 sin、cos 的可以看看下图旋转公式:
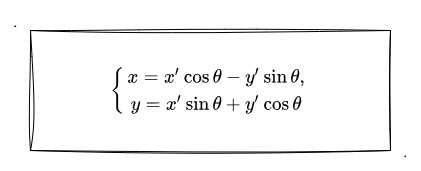
那最后,我们仅需要把 平移矩阵、旋转矩阵 相乘,就能得到我们想要的 模型矩阵 了!所以我们接着找到如下:
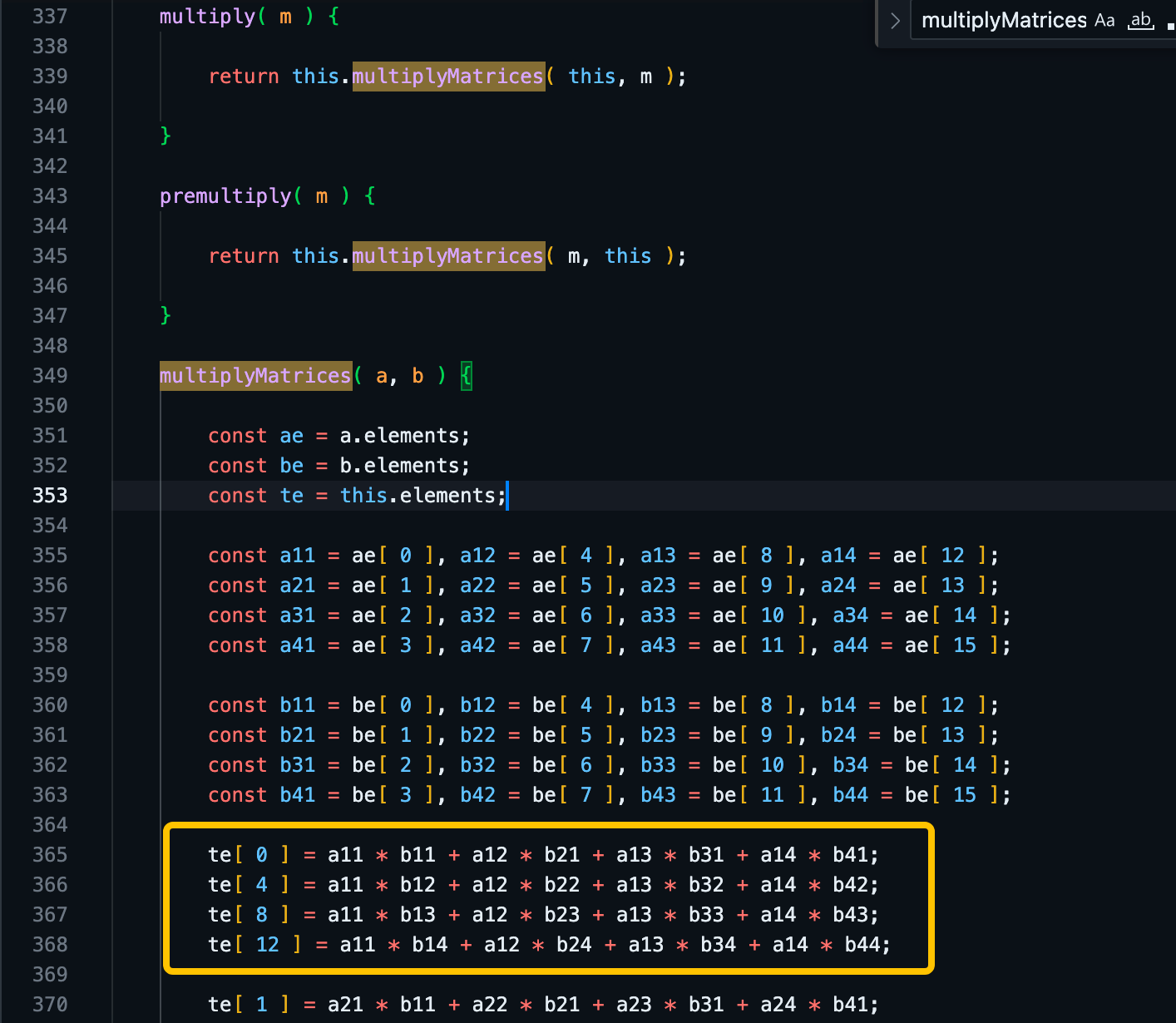
我们看到截图圈了一块黄圈,就是一个行列相乘的计算式。忘记的可以回顾一下 矩阵乘法 :
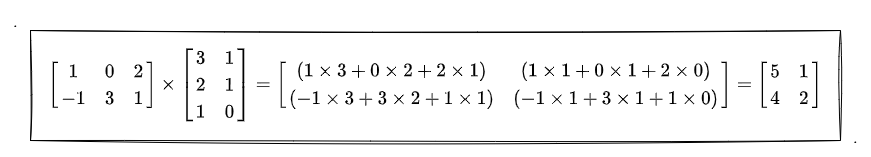
讲到这,我想再次强调一下行列主序的问题。上一节也有强调,怕你们忘了所以再次强调一下:WebGL 的矩阵是列主序的:
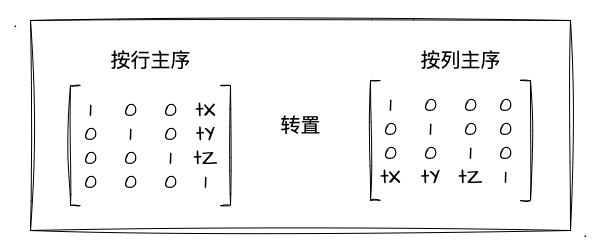
所以,在使用库的时候,我们需要注意什么呢?首先我们要看一下库里面有没有帮我们处理行列主序的问题,如果没有,我们再找找设置矩阵转置的接口,在传递给 WebGL 前调用一下即可。那回到 three.js 中,我们可以看到它内置帮我们做了行列矩阵的转换了,其文档也有提到:
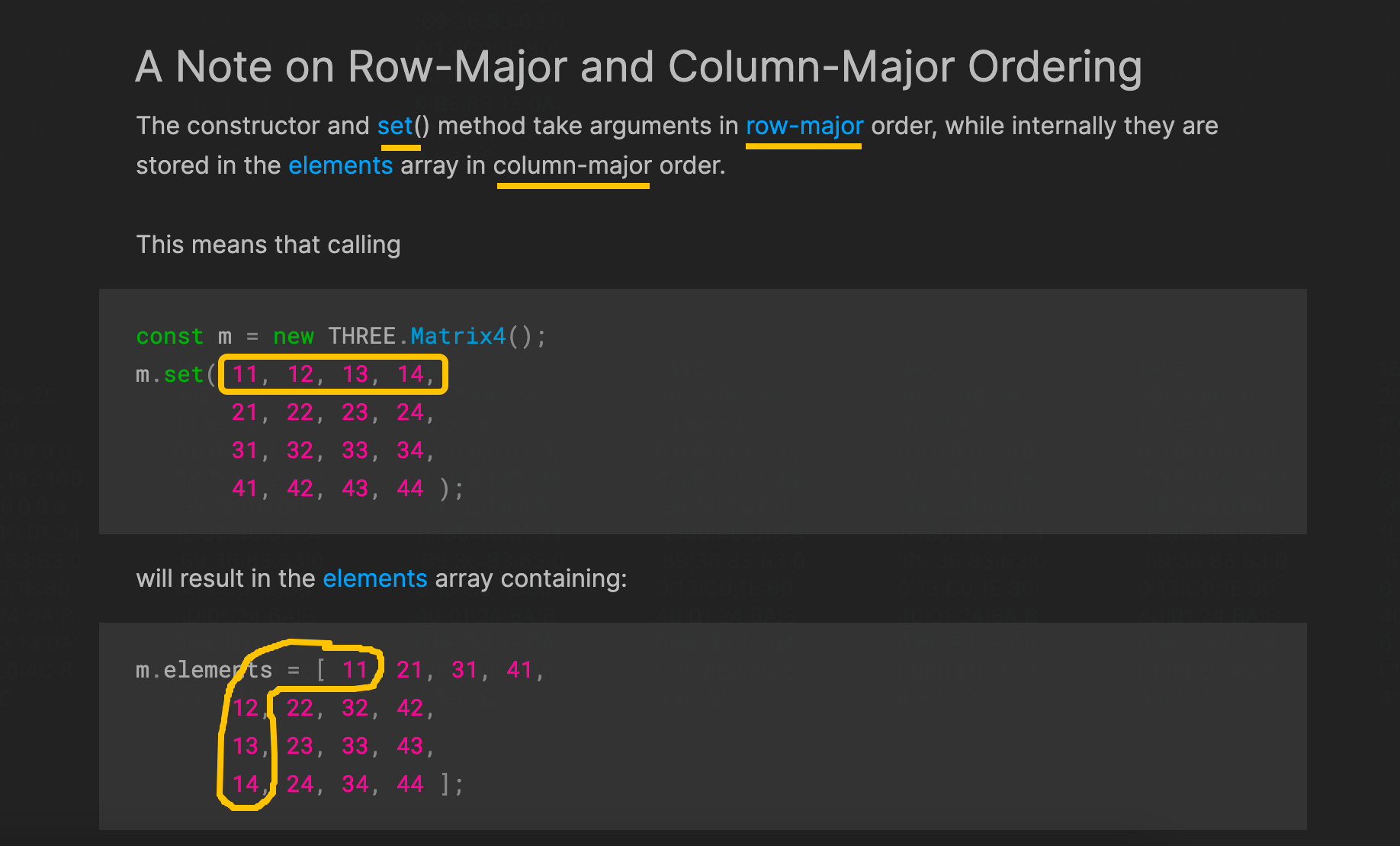
如上图所示,我们用行主序的方式将数据传入构造器、或者使用其原型上的 set 方法,矩阵数据最终会以列主序的方式存在 elements 属性中。
好了,相信大家对于在 JavaScript 中完成矩阵创建、变换、相乘已经有一定了解了,那接下来就可以进入到实战环节了!
三角形的平移&旋转
实战的第一环节首先是我们的顶点着色器代码。当然,经过了本文第一小节的推导,我们的着色器代码跟之前的并无变化,还是可以直接写成矩阵乘矢量:
const vertexCode = `
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
// 模型矩阵(代表平移矩阵和旋转矩阵的积)
uniform mat4 u_ModelMatrix;
void main () {
gl_Position = u_ModelMatrix * a_Position;
v_Color= a_Color;
}
`着色器核心的代码依然是矩阵乘矢量的模式,那么实现复合变换的关键就是 u_ModelMatrix 的值了。前文铺垫了这么多,我们很明白模型矩阵是平移矩阵和旋转矩阵的乘积,所以我们需要的是在 JavaScript 中计算出这个模型矩阵再传到 WebGL 里就行了!
那在第三方库 THREE.Matrix4 类的帮助下,我们的工作变得非常轻松。我们首先创建旋转矩阵:
// new 一个 matrix4 实例
const rotateMatrix = new Matrix4()
// 计算弧度值(rotateVal是滑块的位置)
const radian = rotateVal * Math.PI / 180
// 传入弧度值设置旋转矩阵
rotateMatrix.makeRotationZ(radian)简单分析下:
- 通过
new Matrix4()创建了一个matrix4实例。因为没有传参,此时的elements是个单位矩阵 - 根据
rotateVal角度计算弧度值,它的值在示例程序中由滑块的位置控制(弧度计算公式之前都有讲过) - 通过
makeRotationZ方法设置旋转矩阵。此时的elements就是旋转矩阵了
那么我们还需要创建一个平移矩阵如下:
// new 一个 matrix4 实例
const translateMatrix = new Matrix4()
// 计算位移值(rotateVal跟上面旋转角度用的同一个值)
const translateX = rotateVal / 360.0
// 设置平移矩阵
translateMatrix.makeTranslation(translateX, 0., 0.)上述代码大家可以发现其实跟旋转矩阵的创建是差不多的,所以我就不一一分析了。那此时得到平移矩阵后,我们还需要将其和旋转矩阵相乘就可以得到我们的模型矩阵了。所以!我们继续调 api :
// 平移矩阵 x 旋转矩阵
translateMatrix.multiply(rotateMatrix)那么此时,translateMatrix.elements 已经是一个模型矩阵了。这时候,我们再把这个值通过 uniformMatrix4fv 给到 WebGL,再重新绘制三角形就能实现复合变换的三角形了!
gl.uniformMatrix4fv(u_ModelMatrix, false, translateMatrix.elements)提醒大家要注意的是,THREE.Matrix4 的矩阵值是放在 .elements 属性中的,所以通过 uniformMatrix4fv 传递给 WebGL 的时候要用 xxx.elements。剩下的就没什么好说了,我们直接看看示例程序的效果吧:
可以看到,示例程序中,当我们拖动滑块,三角形不仅在平移,而且还会旋转!(这里注意一点,矩阵乘法不满足交换律,所以平移矩阵、旋转矩阵相乘的先后顺序不同会有不同的变换效果~)
总结
那么本文我们通过实战图形复合变换,更加明白了矩阵在图形学中重要了,最后简单地总结一下:
- 模型矩阵:多个变换矩阵相乘的结果,是复合多种变换的矩阵。在推导模型矩阵的过程中,顺便也复习了一下矩阵的乘法。
- 在 JavaScript 中借助
Matrix4的类库进行矩阵运算,极大简化我们的矩阵操作、运算成本。 - 矩阵乘法一般不满足交换律,变换矩阵的相乘顺序不同可能会有不同的复合变换效果。
 iceWebGL
iceWebGL