5. 实战相机渲染引擎
上一节我们深入地了解并推导了视图矩阵,完全的数学推导多少有点枯燥无味了,所以我们想办法让其炫酷起来。推导得这么辛苦,当然是得实战体验一波效果啦!所以本节将通过 javaScript 实现视图矩阵,实战一个简易的相机渲染引擎!
既然要自己实现一个相机渲染引擎,那肯定有一些需求点的。所以在实战内容开始之前呢,先大概讲讲本次实战要实现的功能:
- 同时平移视点、观察点,实现图形的反方向平移效果
- 仅改变视点,实现不同角度地观察图形
那么,让我们带着上述的两个需求点开始本文的实战内容吧!(建议看过前文视图矩阵推导的再来看本文会更容易理解~)
用js实现视图矩阵
我们要想实现一个简易的相机渲染引擎,毫无疑问首先要用 js 实现一个视图矩阵(而我们的定点着色器核心代码依然是一个坐标点左乘视图矩阵而已)。也就是说,当我们给相机传入不同的 视点、观察点、上方向 数据时,浏览器最终会渲染出不一样的图像呈现在我们面前。
1. 创建ViewMatrix类
首先我们创建一个视图矩阵的 class,并且初始化一个单位矩阵在它的 elements 属性中:
class ViewMatrix {
elements: Float32Array
constructor() {
this.elements = new Float32Array([
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
])
}
}在上述的基础上,我们给 ViewMatrix 添加一个 lookAt 的方法。简单处理,这个方法接收 9 个参数,包含 视点、观察点、上方向 三种数据的 x、y、z 值。直接通过 ts 的定义来看看吧:
// c...代表相机;t...代表观察点;u...代表上方向
interface TLookAt {
(cX: number, cY: number, cZ: number, tX: number, tY: number, tZ: number, uX: number, uY: number, uZ: number): void
}ok,lookAt 方法中,我们就要按照上一节对视图矩阵中 x、y、z 轴的推导转化为 js 中的实现。最终就要实现当给其传入不同的 视点、观察点、上方向 数据后可以得到对应的视图矩阵!我们马不停蹄开始旋转矩阵的实现!
2. lookAt中的旋转矩阵
这里,我们简单回顾一下上一节我们推导出来的旋转矩阵:
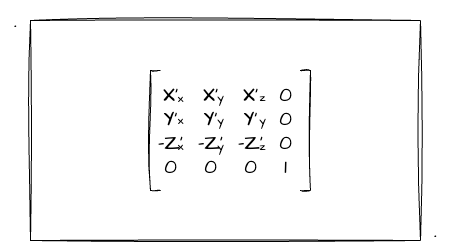
因此,我们需要做的就是把矩阵中 X'、Y'、Z' 的值都求出来就行了。这一点对我们来说并不困难,因为上一节我们对每一个值进行了推导,这里更多的是用 js 套用数学公式来实现而已。
但这里我们要注意一点:WebGL中的矩阵是列主序。这一点之前在矩阵实战图形变换中有提到。因此,在我们实战过程中,我们要把数学推导出的行主序的矩阵做一个转置,以最终传递到 WebGL 中使用。
首先,我们来实现旋转矩阵的Z轴求解。上一节讲过,求两点之间形成的向量,用后者减前者即可(忘记的回顾一下前文)。所以,我们只要把 观察点坐标 减去 视点坐标,求得的就是相机的Z轴。将实现放到代码里,其实就是:
// t...代表观察点;c...代表相机;
zX = tX - cX
zY = tY - cY
zZ = tZ - cZ
// 以下是归一化实现
zToNormal = 1 / Math.sqrt(zX * zX + zY * zY + zZ * zZ)
zX *= zToNormal
zY *= zToNormal
zZ *= zToNormal代码中,使用观察点减视点坐标求得 zX、zY、zZ 坐标后,还做了归一化处理。
那么归一化是什么?为什么要把向量归一化处理呢?笔者是这么理解的:归一化可以将矢量等比例变化,从而转换为单位矢量。因为我们这里要求出的相机的坐标系,所以我们仅需要关注矢量方向,不用关注模长。(感兴趣的朋友自行查阅相关资料吧)
概念性的东西,我们知道就行了,更关键的是我们需要知道怎么用。所以接下来一起看看归一化用公式如何表达。当前,把|Z|记作为Z的模长(模长为Z轴上每个分量的平方相加后再开方);此时把Z轴归一化即为:
Z' = Z / |Z|我在代码中把他们写成 zX *= zToNormal (乘的是一个倒数),其实就是相除法。至于为什么这么写,是有关矢量除法的问题(详细的我也没太了解清楚,求个数学大牛来教学教学)。anyway吧,暂时可以不用在数学上研究这么深入,懂得运用就好。
求得Z轴后,现在我们还有上方向(up坐标值)的数据,于是我们就可以通过矢量叉乘的方式来求出相机的X轴了! 那如何求三维矢量的叉积?我们回顾之前看过的维基百科对矢量叉乘的说明:

我们依着上图的计算公式,把u、v的值替换成我们的 Z轴 和 上方向 就行了。比如说上图的u2换成zY,v3换成uZ以此类推...好了,话不多说,直接上代码:
xX = zY * uZ - zZ * uY
xY = zZ * uX - zX * uZ
xZ = zX * uY - zY * uX
// 进行归一化处理
xToNormal = 1/ Math.sqrt(xX * xX + xY * xY + xZ * xZ)
xX *= xToNormal
xY *= xToNormal
xZ *= xToNormal如上代码块所示,我们通过叉乘就求出了相机的X轴,现在就剩下相机的Y轴了。相机的Y轴不就是我们传入的上方向吗?那是不是直接用上方向来充当相机的Y轴就行了呢?
答案是不行。不得不说,其实我一开始也是这么认为的,但其实不然。我们通过代入一个例子来理解这一点,现比如相机坐标系就是世界坐标系,上方向为Y轴,垂直于X、Z形成的平面。此时如果我们调整了视点、观察点的位置,导致整个世界坐标系发生了旋转,那Y轴是不是也要跟着转呢?
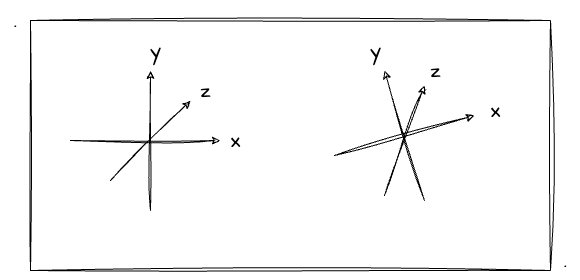
如上图,当调整了视点、观察点数据后(坐标系发生旋转),可能会导致上方向不再是(0,1,0)了,但它依然是保持着垂直于X、Z平面!说到这里,已经第二次提到Y轴垂直于一个面了,所以大家应该也能码上想到,求出相机的Y轴也就是将Z轴和X轴做叉乘法即可!我们直接看结果:
yX = zZ * xY - zY * xZ
yY = zX * xZ - zZ * xX
yZ = zY * xX - zX * xY如上所示,我们通过X、Z轴的叉乘求出Y轴。可能有同学发现了这里并没有做归一化处理,因为用于叉成的坐标轴已经是归一化后的坐标值了~
目前,我们已经完成了旋转矩阵 X、Y、Z 轴三轴的计算,接下来我们就把结果放到矩阵中吧。应该还记得我们初始化时候定了一个4x4单位矩阵的一维数组吧:
this.elements = new Float32Array([
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
])现在我们就把计算,通过数组下标往里面替换就行了!但是这里我们依然要注意一点:WebGL中的矩阵是列主序。所以我们这里替换的时候,一定要记得是要以列主序的方式写入数据的。如图:
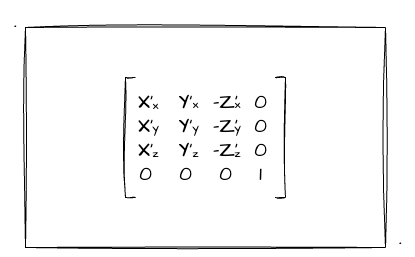
对着上图,我们一一代入数据就行了!这里还要注意一个点,图中的 Z值需要传入一个负值(具体的分析在前文也已经分析过了,还不理解的可以回去前文看看),所以记得把Z相关值传入的时候取一个负数!
const e = this.elements
e[0] = xX
e[1] = yX
e[2] = -zX
e[4] = xY
e[5] = yY
e[6] = -zY
e[8] = xZ
e[9] = yZ
e[10] = -zZ注意一点,e[3]、e[7]、e[11] 位置在旋转矩阵中是不需要用到的,是下文讲到的平移矩阵需要用的。
3. lookAt中的平移矩阵
我们都知道,视图矩阵中的平移矩阵非常简单,就是把相机移动到世界坐标轴的原点即可。只需要把传入的 cX、cY、cZ 取负再放到对应的位置就可以了。这里我们更重要的是处理旋转矩阵跟平移矩阵相乘后的值!
回顾上一节我们推导的最后结果:
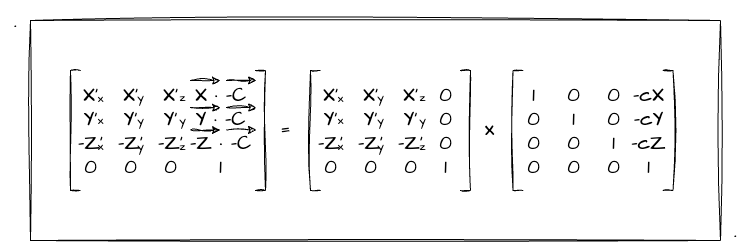
其实这里的计算也不难,我们只要把旋转矩阵的 X、Y、Z矢量 一一乘上视点矢量即可!依然需要我们注意的就是列主序这件事,我们计算完的结果要通过列主序的方式放到 elements 属性中。矢量叉乘计算之前也有讲过了,这里就不再展开了。我把乘上平移矩阵的步骤放到一个方法 multipleTranslateMatrix 里,我们一起看看结果:
multipleTranslateMatrix (cX: number, cY: number, cZ: number) {
const e = this.elements
e[12] += e[0] * cX + e[4] * cY + e[8] * cZ
e[13] += e[1] * cX + e[5] * cY + e[9] * cZ
e[14] += e[2] * cX + e[6] * cY + e[10] * cZ
}以上便是整个视图矩阵的代码实现了。另外提一下,关于 e[15] 的值,因为这两个矩阵相乘后它的值一直都是1,所以这里让他维持初始时候的1即可。
到最后,我们简单地回顾一下视图矩阵的整体代码框架:
lookAt (cX: number, cY: number, cZ: number, tX: number, tY: number, tZ: number, uX: number, uY: number, uZ: number) {
let xX, xY, xZ, yX, yY, yZ, zX, zY, zZ, xToNormal, zToNormal
// 1. 求 Z 轴
zX = ...
// 2. 叉乘求 X 轴
xX = ...
// 3. 叉乘求 Y 轴
yX = ...
// 4. 乘上平移矩阵
this.multipleTranslateMatrix(-cX, -cY, -cZ)
}实战视图矩阵变换
前文,我们顺利通过 js 自己实现了视图矩阵类——ViewMatrix。接着我们就直接在实战中应用,看一看效果。因为要凸显出相机旋转时候的效果,我这里在Z轴上画三个大小相等,位置稍微不等的三个三角形(Y轴递增),并且他们的深度数据不同。
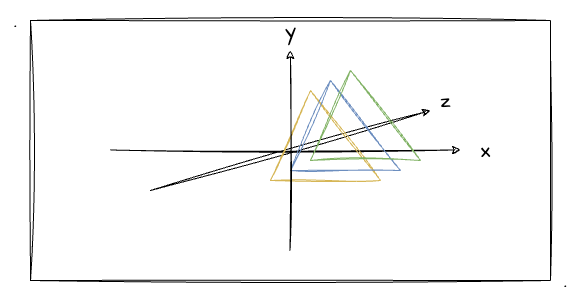
如上图所示,这就是这次我们绘制黄、蓝、绿三个三角形,并且黄色在Z轴的最前面,绿色在最后面。这里我们先不管深度测试,我们直接按照WebGL的默认绘制行为就行了(后绘制的覆盖先绘制的图形)。也就是说,我们要先录入绿色三角形的数据,再到蓝色、最后是黄色。数据如下:
const vertices = new Float32Array([
// 绿
0, 0.6, -0.6, 0.45, 0.82, 0.24, 1,
-0.5, -0.4, -0.6, 0.45, 0.82, 0.24, 1,
0.5, -0.4, -0.6, 0.45, 0.82, 0.24, 1,
// 蓝
0, 0.5, -0.4, 0.086, 0.53, 1, 1,
-0.5, -0.5, -0.4, 0.086, 0.53, 1, 1,
0.5, -0.5, -0.4, 0.086, 0.53, 1, 1,
// 橙
0, 0.4, -0.2, 0.98, 0.68, 0.078, 1,
-0.5, -0.6, -0.2, 0.98, 0.68, 0.078, 1,
0.5, -0.6, -0.2, 0.98, 0.68, 0.078, 1,
])数据定义好了,我们再来看看顶点着色器怎么写:
const vertexCode = `
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
uniform mat4 u_ViewMatrix;
void main () {
gl_Position = u_ViewMatrix * a_Position;
v_Color= a_Color;
}
`细看代码发现,其实跟之前没什么两样~依然是外部传入的坐标数据 a_Position 左乘视图矩阵 u_ViewMatrix。然后这里通过 varying 变量传递颜色值到片元着色器。
这些我们之前都很熟悉了~紧接着,我们来看以下使用我们自己封装的视图矩阵 ViewMatrix 的写法。首先定义了三个初始的一维数组,分别代表相机位置、目标观察点、上方向:
const camera = [0, 0, 0]
const target = [0, 0, -1]
const up = [0, 1, 0]有了以上的数据,我们按照之前设计的 lookAt 用法,把每一个参数对应地传给该方法就行了!因为这里我定义的时候采用了数组的形式定义数据,所以在传入值的时候,为了方便,我采用了 js 中的 apply 函数!
const matrix = new ViewMatrix()
// 用 apply 方便传入数组数据
matrix.lookAt.apply(matrix, [...camera, ...target, ...up])
// 把视图矩阵传入顶点着色器中使用
gl.uniformMatrix4fv(u_ViewMatrix, false, matrix.elements)关于其他部分,都跟之前学习过程的2D图形绘制没什么区别了,最后也是用 gl.drawArrays 进行图形的绘制。有需要看详细源码的同学就自行点出源码查看即可!
那么,接下来简单介绍一下示例程序中的功能和效果:
- 同时改变相机和观察点位置。类似于把相机平移,此时场景会向着相机的反方向平移(可以自行脑补一下是不是这样的)。
- 仅改变相机位置。这个就类似旋转了,固定观察点,改变相机位置可以切换我们的观察角度,使图形发生旋转效果。
总结
本文的最后,跟大家一起回顾本文的主要内容:
- 实战视图矩阵中旋转部分的代码实现。其中了解了归一化的知识点,并且明白了相机的
X、Y、Z轴是如何计算出来的。 - WebGL中的矩阵是列主序。虽然这一点之前我们就了解过了,不过一只没有实战应用过,所以可能印象不深。经过本文就应该对列主序有更深的印象了。
- 同时平移相机、观察点时,相机实现平移,而场景图形则反方向平移;仅改变相机位置旋转相机时,场景图形反方向旋转。
 iceWebGL
iceWebGL