7. 透视投影 ​

经过上一节的学习，我们已经了解并实战使用了投影之一的正交投影！那么本节，我们趁热打铁，把更贴近生活场景、更接近视觉效果，并且也是更难的透视投影也一探究竟吧！

了解透视投影 ​

那么上一节也有提到透视投影，它更贴近生活，符合我们人的视觉效果，会有近大远小的现象。当然，这种投影的使用程度也是更加的广泛。跟上一节学习的正交投影的可视空间是长方体的不同，它的可视区域是一个类四棱锥，我们可以通过下图来回顾一下（左图）：

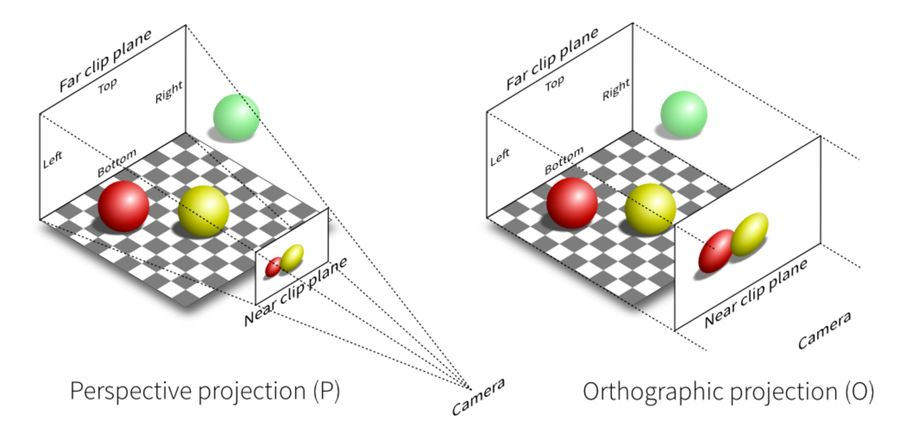
由上图（左）可以发现，透视投影的可视区间是四棱锥中的远近裁剪面决定的，近裁剪面跟远裁剪面之间形成了一个四棱台（近裁剪面小于远裁剪面）。并且图像会投影到近裁剪面上，这也是最终呈现在显示器上的图像结果。

这里，我们跟上一节一样，通过图、描点的方式，把透视投影的可视区域表达出来！当然，因为它不再是长方体结构，所以我们要分别对远近裁剪面进行描点～如下图：

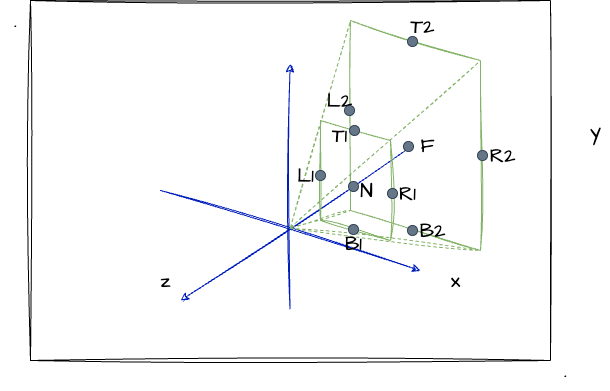
上图中，我们依然通过 left、right、top、bottom、near、far 点位对透视投影的可视区域进行描述。与正交投影的不同的是，远近裁剪面大小不相同，所以对于 top、bottom、left、right 值我们分别对两个面进行标注。

这里我们可以试想一下，如果我们将远裁剪面进行一定的压缩，变成跟近裁剪面等大的长方形，那可视空间不就又回到了我们熟悉的长方体了吗？如此一来，只要我们把这个长方体移动到世界坐标原点吗，再缩放到[-1, 1]区间范围，不就是我们刚学完的正交投影变换吗！

所以，我们应该如何构造出这个长方体？简单来说就要压缩远裁剪面，把它压成近裁剪面大小。

比如说现在空间中有一个点A(x, y, z)，我们要做的就是把x压缩成xA，把y压缩成yA。我们先不着急想要怎么压缩，先找找透视投影可视区域有什么样的规律或者特性。比如现在我们从正侧面观察这个四棱台的特性：

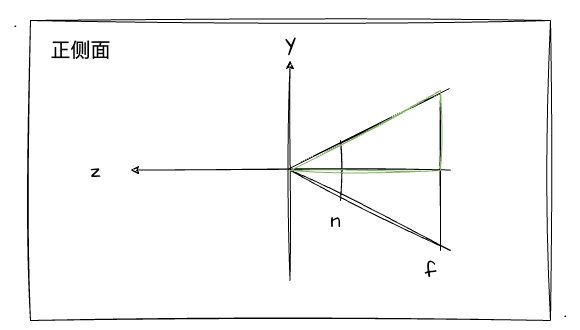
上图中我描了绿色边的三角形在我们的九年义务教育中它叫啥？相似三角形有没有？那相似三角形的特性之一：三组对应边均成比例对此至关重要！为什么这么说？我们接着把案例（点A）代入进图中观察：

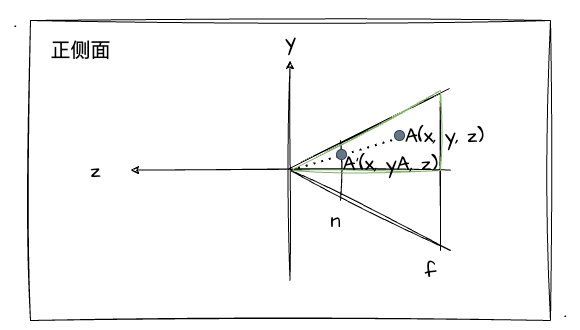
如图，当我们把A点进行压缩时，它最终压缩到的对应位置为A'，那此时，它的Y轴坐标将由原来的y变为yA。由于A'和A围成三角形为相似三角形，所以对于y轴的压缩值，我们可以通过以下等式来表示：

// z是A点的z坐标值，n是近裁剪面的z坐标值；
z / n === y / yA
// 变换为：
yA = y * (n / z)

也就是说，对于变换后的 yA 来说，它的值等于 y 乘 n/z 的结果。同理，我们以同样的方式对X轴的坐标值进行转换。比如现在我们从正上方观察四棱台：

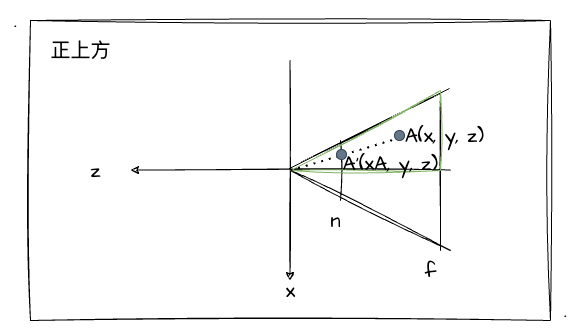
没错，跟从正侧面的规律是一样的，依然是相似三角形，依然是有三组对应边均成比例这个重要特性。并且，我们通过推导可以发现，X跟Y轴坐标的变换公式其实是一样的：

// z是A点的z坐标值，n是近裁剪面的z坐标值；
z / n === x / xA
// 变换为：
xA = x * (n / z)

因此，我们可以得出一个结论：对于可视空间四棱台中每一个坐标的x、y值都乘上 n/z，就可以把这个四棱台变换成一个长方体了！

透视投影矩阵 ​

根据前文做的推导，我们得知将透视投影的四棱台压缩成长方体其实就是将所有的x、y坐标值值都乘上 n/z，于是我们可以将值直接代入到矩阵当中：

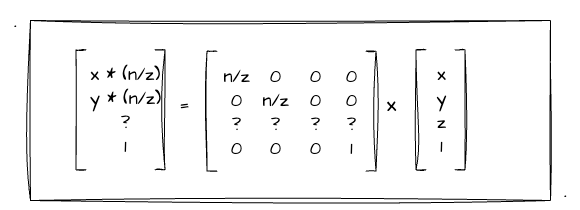
没错，我们仅仅对x、y的值进行代入，毕竟我们还没有求跟Z轴变化有关的值，所以z值（矩阵第三行）相关的位置都是？。那我们有没有办法从已知的信息中来推导这一行的未知数呢？这里我们回顾一下之前第二章学习过的WebGL绘制点中提到的齐次坐标，它的特性是： (x, y, z, w) 其实等价于三维坐标 (x/w, y/w, z/w)。

因此，我们可以推导出齐次坐标(x, y, z, w)等于(xn, yn, zn, wn)，四个分量同时乘上一个常量值n依然是等价的！所以，我们可以给前文求到的齐次坐标的每一个分量都乘上一个z值，可以得到：

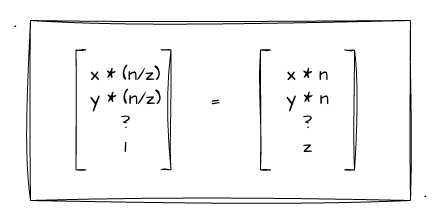
这样有什么用呢？别急，我们接着往下看。当我们给齐次坐标得每个分量都乘上一个z值后，再将其代入到矩阵乘法中，我们可以把矩阵中的z消除！如下图：

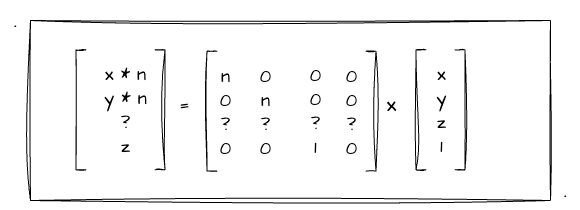
由上图，我们可以看出跟首次推算出来的矩阵有所不同，矩阵中第一、第二行已经没有了z的值，并且矩阵的最后一行也变成了 0 0 1 0。由此，这个变化后的矩阵乘上其次坐标后正好满足 [xn, yn, ?, z] 的结果。接下来，我们需要想办法把第三行的?值求出即可，也就是要考虑z值的变化！

我们已知近裁剪面的z值为n，远裁剪面的为f，且他们为负数，满足 f < n < 0。并且，我们将四棱台变换成长方体的过程中，远近裁剪面的z值是不会发生变化的。现在假设有近裁剪面的一个点(x1,y1,n)和远裁剪面一个点(x2,y2,f)，我们将他们代入上述推断的矩阵中，他们应该满足如下等式：

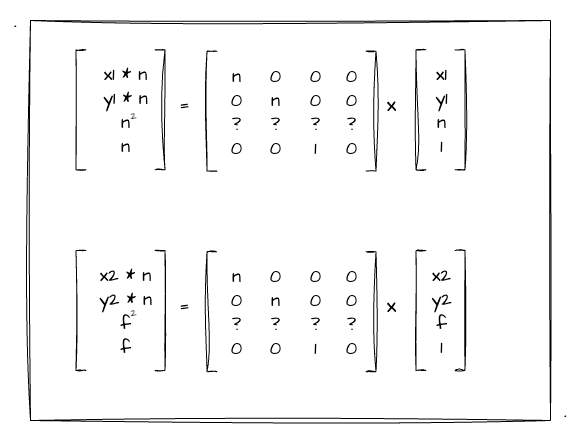
我们按照矩阵乘法单独把第三行的计算抽出来，可以得到如下的关系式：

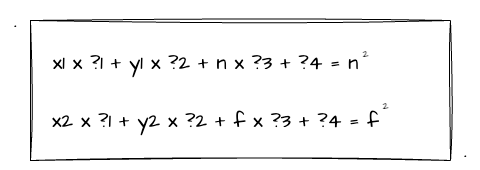
其次，远近裁剪面的z值跟x、y是无关的，所以我们可以把 ?1、?2 设置成0，于是简化后我们可以得到一个相对简化的等式：

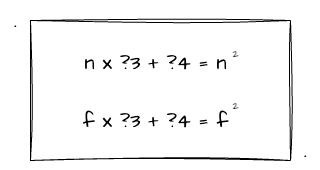
因此，我们可以推出：?3 = n + f，?4 = -nf。我们将其代入到上述的矩阵当中，可以得到如下矩阵：

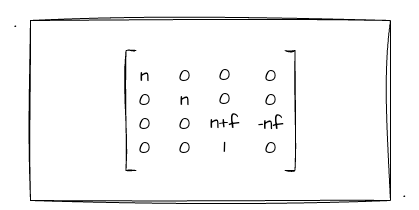
经过这个矩阵的变化，我们已经将四棱台变换成一个长方体了，那最后的透视投影矩阵还差一把就是把这个长方体给标准化了。这么说好像很抽象，其实不然，只要将其再乘上我们上一节所推导的正交投影矩阵就可以了！这里我就不展开了，直接给结果：

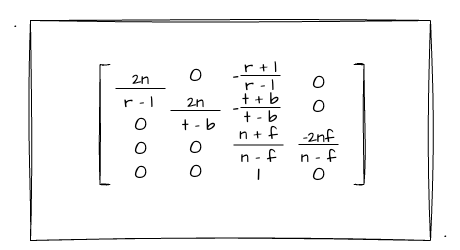
如何表示透视投影？ ​

透视投影如何表示，或者说如何配置呢？回顾一下我们上一节是如何配置正交投影矩阵的？是不是直接通过 left、right、top、bottom、near、far 这些点位的相关值来配置的呢？但是透视投影并不是使用这些来表示和配置的，而是使用 fov、aspect、near、far 这四个值。我们简单看看他们分别是什么。

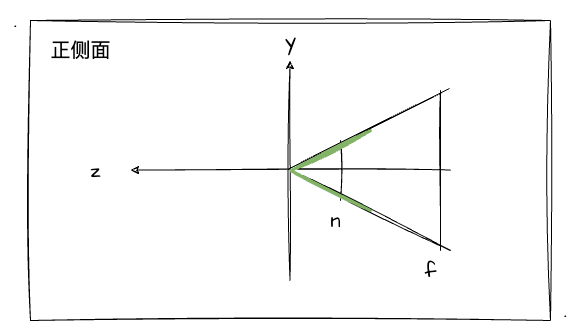
• fov：垂直方向视角，角度越大，视野越广，物体越小。具体可参考下图的绿色角
• aspect：近裁剪面的宽高比。width / height
• near、far：指定近、远裁剪面的位置。值必须要大于0 ，因为它们都是相对于相机的距离。

再回到我们之前的一张图中：

如上图，对应 fov 的角为 T1-原点-B1。并且，根据图我们可以知道，我们把四棱台放到正中间的时候，远近裁剪面都满足 right等于-left，top等于-bottom。所以，我们可以把r-l变为2r，t-b变为2t。于是，我们可以把前文推导出来的透视投影矩阵再做进一步的简化如下：

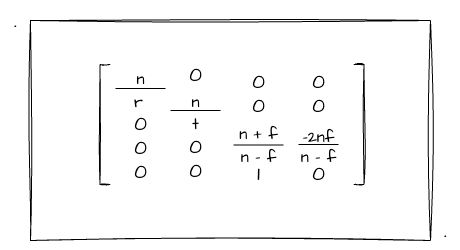
还记得前面我们设 fov 为θ的这一值吗？我们通过三角函数可以得到如下等式：

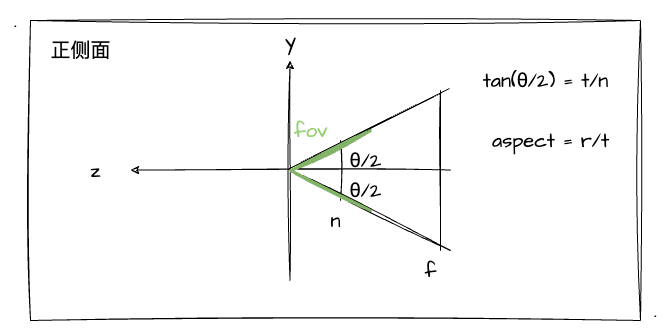
根据换算出来的等式，我们将其代入上述的矩阵中，可以将其完全转化成通过 fov、aspect、near、far 这四个值来配置。具体换算过程我就不逐步演示了，有兴趣的同学可以自行推导。直接看结果：

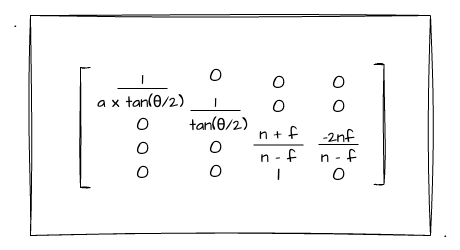
上图即为 fov 为 θ，宽高比为a时的透视投影矩阵了。但是！这就完了吗？这里跟上一节一样，我们依然需要将NDC的Z轴做一次翻转。原因上一节也说过了，就是NDC是左手坐标系，而我们之前一直都在使用右手坐标系来绘制，所以这里依然要做一个转换。具体过程就不在这里展开了，感兴趣的朋友可以自己去试试，直接给出结果吧：

实战透视投影 ​

经过前面几节的学习，相信实战部分应该是最简单的环节了，毕竟只要矩阵推导出来，我们只需要对位置计算就行了。所以这一小节，我不会再深入地介绍示例程序的源码实现了，只会提一下跟之前稍有不同的地方。

为了更加凸显"近大远小"的特点，这里我把三角形的位置做了一点改变，分别将他们相对的移动到左上方，并且把他们的深度从原来的[-0.2, -0.6]调整为[0, -2]。现在的三角形坐标如下（关注Z轴即可，依然省略了颜色值）：

const vertices = new Float32Array([
  // 绿
  -.7, 0.8, -2,
  -1.2, -0.2, -2,
  -0.2, -0.2, -2,
  // 蓝
  -.1, 0.6, -1,
  -.6, -0.4, -1,
  .4, -0.4, -1,
  // 橙
  0.5, 0.4, 0,
  0, -0.6, 0,
  1, -0.6, 0,
])

上述三组三角形数据中，三角形是等大的且深度递增，为了方便观察，我让他们在x、y上进行了一定的偏移。又因为前文提到过 near、far 的值需要大于0，这里我把near设置为1，far设置为5（这个看情况自己定义，本案例中设置5足够了）。

至于fov的设置，大于0即可，我随便设置个60吧（视角设置越大，图像呈现越小），于是乎，关于透视投影矩阵的配置参数也就出来了：

const fov = 60
const near = 1
const far = 5
const perspectiveMatrix = new PerspectiveMatrix()
perspectiveMatrix.setPerspective(fov, gl.canvas.clientWidth / gl.canvas.clientHeight, near, far)

在定义好透视投影矩阵的相关配置后，我们还需要考虑一个问题，那就是相机的设置。前文提到，near值的配置指的是近裁剪面距离相机的位置，这里我们的near设置为1，而又因为我们场景图形的z值是从0开始的，为了可以观测到"最靠前"的橙色三角形，我们需要把相机深度的位置设置为大于1（这跟裁剪空间的范围有关），这里我就设置为2了！这一点大家根据自己的场景自己调整即可，这里方便理解，我画了张图：

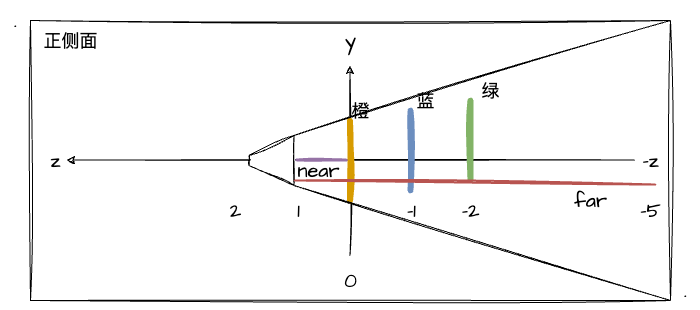
于是乎，我们就可以基于上述的配置，将我们的三个三角形渲染出来，并且可以观察一下透视投影下的他们是怎么展示的。为了做对比，我还添加了正交投影的效果，大家可以切换的来看。这里的正交投影大家可以自己改一下参数试试效果，不同的参数情况下图形会有不同的伸缩效果。

由上示例程序可以看出，在正交投影下我们看到的是三个等大的三角形，只是互相之前存在一定的偏移值；而透视投影下则是三个三角形大小呈递减趋势，呈现明显的近大远小的效果！这里我建议大家手动调整一下示例程序里面的参数，再观察一下效果是不是跟自己的预期一样，以此来验证一下学习的成果。当然，如果你自己动手写一个效果会更好～

总结 ​

本文的最后，跟大家一起回顾本文的主要内容：

1. 透视投影中，图形呈现近大远小的效果，近裁剪面为最终的屏幕呈现效果
2. 透视投影的核心变换即将四棱台转压缩长方体（以近裁剪面为基准），然后再进行正交投影变换即为透视投影变换
3. 透视投影推导过程中，巧妙利用 齐次坐标的第四个参数w 来消除矩阵中的未知z值
4. 通过 fov、aspect、near、far 四个参数值来表达一个透视投影的裁剪空间，且 near、far值均大于0