2. 深入立方体的绘制
上一小节中,我们实战了一个渐变色立方体的绘制,学习了新的绘制api,但是在文章的结尾,我留下了个疑问,就是如何绘制一个6面为不同纯色的立方体呢?那我们这一节将继续探讨关于立方体的绘制!
构造立方体数据
那么,上一节的文末我简单分析了一下仅用 8 个顶点来绘制立方体无法实现六面为不同纯色立方体的原因。那这里,我们配合图片来加深一下理解:
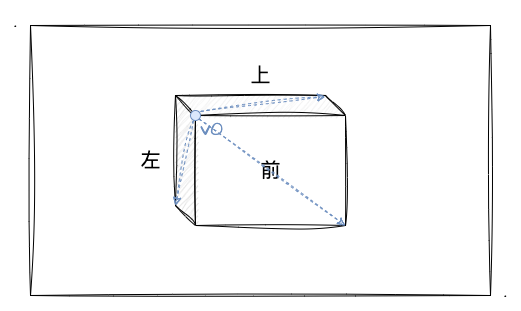
如图所示,如果仅使用 8 个点来绘制立方体的时候,蓝色顶点 v0 将被 前、上、左 三个面共享。也就是说只要当前面的其他顶点颜色跟 v0 的不同,那一定会被 WebGL 的内插行为致使那个面产生一个颜色渐变的效果。
所以基于以上的分析,我们如果要实现六面为不同纯色的立方体,那就不能出现公共点。也就是说我们不能出现一个点被多个面公用的情况!因此我们就需要将立方体的每个面分别绘制,那么一个面至少得用 4 个点来表示,六个面总共需要 24 个点~
现在我们来看看上一小节渐变立方体的顶点、颜色和索引值的数据:
// 顶点坐标
const vertices = new Float32Array([
-.5, .5, .5, // v0
-.5, -.5, .5, // v1
.5, -.5, .5, // v2
.5, .5, .5, // v3
.5, .5, -.5, // v4
.5, -.5, -.5, // v5
-.5, -.5, -.5, // v6
-.5, .5, -.5, // v7
])
// 颜色值
const colors = new Float32Array([
1., 1., 1., 1.,
1., 1., 0., 1.,
1., 1., 1., 1.,
1., 0., 1., 1.,
0., 1., 1., 1.,
0., 0., 1., 1.,
1., 1., 0., 1.,
0., 1., 1., 1.,
])
// 索引值
indices = new Uint8Array([
0, 1, 2, 0, 2, 3, // 前
3, 2, 5, 3, 5, 4, // 右
4, 5, 6, 4, 6, 7, // 后
7, 0, 6, 0, 1, 6, // 左
0, 3, 4, 0, 4, 7, // 上
1, 2, 5, 1, 5, 6 // 下
])其实列了一大堆数字,我并不是要大家去看这一个个数字,而是需要大家能一一对应得上每行数据之间的关系。我们重点看 vertices 顶点坐标数组 和 indices 索引数组。这里 vertices 总共有 8 个顶点坐标数据,并且在 indices 索引数组中,通过 0-7 的索引一一对应上了每个顶点坐标。
大家可能也注意到 indices 索引数组中每行数据后都有注释表明这一堆索引是组合立方体的哪一个面的。那基于前文的构造六面不同纯色立方体的顶点个数分析,如果我们要用 24 个顶点坐标来绘制立方体,显然上述的 vertices 顶点坐标数组的坐标个数是不够的~
所以,我们需要把 vertices 数组的顶点坐标数扩充到 24 个,并且我们通过 0-23 的索引值,重新组织六个面以形成一个新的立方体。当然啦,别忘了我们还要给每个面设置颜色,所以 colors 数组中的颜色 RGBA 值也是要匹配对应的 24 个。
那么为了让大家更清晰地看出每个独立面的配置,我把顶点坐标、颜色放置在同一个数组中,最后通过步进参数、偏移参数(忘了的赶紧回顾下三、1. 绘制彩色的三角)完成对不同类型的数据进行读取。
const vertices = new Float32Array([
// 蓝(顶点坐标 + RGBA)
-0.5, -0.5, 0.5, 0.98, 0.86, 0.078, 1, // 0
0.5, -0.5, 0.5, 0.98, 0.86, 0.078, 1, // 1
0.5, 0.5, 0.5, 0.98, 0.86, 0.078, 1, // 2
-0.5, 0.5, 0.5, 0.98, 0.86, 0.078, 1, // 3
// 绿(顶点坐标 + RGBA)
-0.5, 0.5, 0.5, 0.45, 0.82, 0.24, 1, // 4
-0.5, 0.5, -0.5, 0.45, 0.82, 0.24, 1, // 5
-0.5, -0.5, -0.5, 0.45, 0.82, 0.24, 1, // 6
-0.5, -0.5, 0.5, 0.45, 0.82, 0.24, 1, // 7
// 全部数据大家请移步到示例程序的源码中查看吧
...
])如上代码块可以看出,现在我们通过 4 个顶点来描述一个面,换句话说就是索引从 0-7 仅仅也就描述了两个面,所以要描述完整个立方体需要 0-23 的索引值。于是我们可以看看现在的索引值数组:
// 索引从 0-7 变成 0-23
indices = new Uint8Array([
0, 1, 2, 0, 2, 3,
4, 5, 6, 4, 6, 7,
8, 9, 10, 8, 10, 11,
12, 13, 14, 12, 14, 15,
16, 17, 18, 16, 18, 19,
20, 21, 22, 20, 22, 23
])通过这样的数据配置,我们就能实现一个六面不同纯色的立方体了,也就是我们上一小节开头的立方体。示例程序如下:
实战线立方体
那么,在了解了索引构造立方体后,为了加深大家的印象,我们接着实战一个由线段组成的立方体。我们简单回顾之前绘制基础图形时关于线段绘制的 mode :
gl.LINES绘制单独的线段gl.LINE_STRIP绘制连接的线段gl.LINE_LOOP绘制连接的线段,最后一个点会和第一个点连接
那么上述的三种 mode,不管我们选用哪一种都可以实现我们的线立方体,只是要组合使用的顶点数据不同而已。那这里,我以 gl.LINE_STRIP 为例来实战线立方体。首先我们接着回顾上一节中的一个顶点坐标图:
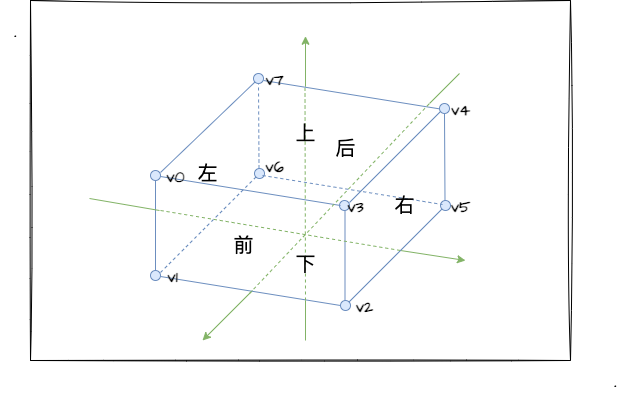
我们只要按照点和点之间的顺序把顶点连接起来,只要最后形成一个闭合的图形,那就大功告成了。比如 v0、v1、v2、v3 配合 v3、v2、v5、v4 就可以形成如下的图形:
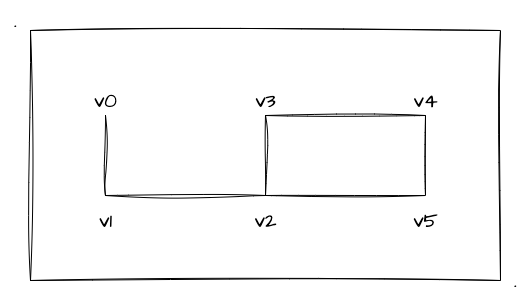
没错,只要我们慢慢推导,最后能形成一个全闭合的六面体就行了。这里我再提醒一下,目前处于学习阶段呢,最好自己推导一下索引值加深印象(顺便加深对 gl.LINE_STRIP 等 mode 的理解),即使以后的实战中我们可以通过工具来生成模型...
再推导索引值顺序的过程中,我们要注意一下面与面连接之间的处理,避免出现斜线连接就行了(比如下图)。最后,虽然有些线段之间是重合的,但是我们看起来是一个完整的线立方体也是无伤大雅的,毕竟没人看得出来哪里重合了~

好了,具体的推导我就不一一讲解了,我们直接看示例程序吧:
深度测试
上一节中,我一笔带过了一个绘制 3D 图形的小点——深度测试,通过 gl.enable(gl.DEPTH_TEST) 这个 api 来 开启隐藏面消除。因为简单的带过,所以大家可能没 get 到这一个点,这里我们深入一下其中的细节。
这里我们思考一下,当我们把 3D 的图形通过 2D 的屏幕来展示,那势必要处理好各图形"深度"之间的关系。也就是说图形在 Z 轴上先后顺序会决定某些靠后的面被其他面遮挡的这么一个情况。
为了让大家有个直观的体验,我直接在本文的六面纯色立方体中做个小改动如下:
根据示例程序的表现,大家可以看出来没有启用深度测试的时候,立方体的表现非常奇怪,会出现同一个视觉中,靠后的面挡住靠前的面的情况。
这是因为 WebGL 默认按照缓冲区数据的顺序来绘制,那么先绘制的面就会给后绘制的面覆盖。那么这个时候有同学会说,那我控制好缓冲区的顶点数据顺序或者索引顺序,再绘制不就行了吗?emmm,好像也可以,但是如果我换个角度观察(比如旋转了立方体),那你是不是得重新排序多一次顶点的顺序呢?
于是乎就有 深度测试 ~深度测试的意思就是根据每个几何图形在 Z 轴上的"深度",来计算它们之间的前后关系,根据"距离眼睛远处被近处遮挡"的自然现象来实现不绘制会被隐藏的面,也就是消除隐藏面~
我们可以这样简单理解,深度测试类似图形装配、光栅化等流程。经过深度测试过程时,WebGL 可以根据各图形在 Z 轴上的前后关系来丢弃一些像素,以实现隐藏面被遮挡的效果。
总结
本文更多是针对上一节的内容进行一个加深巩固,通过实战六面不同的纯色立方体和线立方体,跟大家一起更加深入地了解了关于 索引值 的实战使用,也顺带回顾"消失"了一段时间的线段绘制。最后还提了提深度测试 gl.enable(gl.DEPTH_TEST) 对于绘制 3D 图形的作用和它的基本原理。
 iceWebGL
iceWebGL